蒸汽流量計量中關于管道蒸汽渦街計量表的特性分析研究
管道蒸汽渦街計量表在測量液體和氣體方面都有很好的應用，針對于管道蒸汽渦街計量表在蒸汽流體上的測量，近年來得到了很廣泛的推廣，許多儀表生產企業也在積*地攻關與研發。對于蒸汽了測量一直是比較棘手的，為了強化對于蒸汽的計量能力，在20世紀60年代，日本橫河電機株式會社與美國Eastech公司合作，共同研發了一種管道蒸汽渦街計量表，它的耐高溫性能好，壓損不大，這種流量計廣泛應用于高溫條件下蒸汽流量的計量過程。因為流體流量和其輸出的頻率信號存在正相關性，同時頻率信號在流體組分、密度、壓力、溫度改變情況下仍能保持一定穩定性；另外，此儀器的量程較大；均為不可動部件，穩定性大大增強；結構相對簡單，安裝維護難度小，維護成本低。基于以上優點，該頻率信號被普遍使用在計量與工業過程的控制過程中。
到了二十世紀80年代，因為工業生產的推動，管道蒸汽渦街計量表得以廣泛采用，但缺點是對于蒸汽介質上的測試仍是空白，只可進行管道蒸汽渦街計量表的構造方式、DSP、流量量程、管道材質等方面加以升級，增強了管道蒸汽渦街計量表的在液體與空氣中的測量準度。由于在蒸汽介質方面的探索上存在盲區，在流量精度測量上長期以來備受業內人士的質疑。管道蒸汽渦街計量表雖然技術上有了改進，但有待進一步改良，不管是在理論還是應用層面上均有諸多工作要做。近些年，**范圍內的業內人士對于管道蒸汽渦街計量表實施了多次探索，研究成果值得肯定。
蒸汽流量量值體系的溯源是保證蒸汽流量測量準確的關鍵。本文基于流體力學、熱力學以及管道蒸汽渦街計量表旋渦的產生機理，分析不同介質對管道蒸汽渦街計量表的計量特性的影響，介質粘度的不同導致了三種介質測試下雷諾數的不同，影響到斯特勞哈數差異。但對管道蒸汽渦街計量表的儀表系數影響不大，可忽略其影響。介質粘度的不同會導致流量范圍的不同。該分析將有利于提高管道蒸汽渦街計量表測量蒸汽流量的計量準確度。
1 蒸汽介質的影響因素
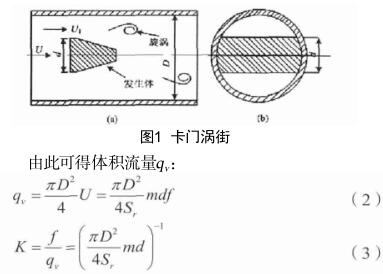
所謂管道蒸汽渦街計量表(亦稱旋渦流量計)，其工作機理是“卡門渦街”，是一類流體振蕩式的測量儀器。“卡門渦街”的原理是：待測管道流體中放進一根(或數根)非流線型截面的旋渦發生體，等到雷諾數到達特定數值，在旋渦發生體兩側分離出兩串交錯有序的旋渦，此過程具有交替性，我們將這種旋渦叫作卡門渦街。在特定雷諾數范圍之間，旋渦的分離頻率同旋渦發生體與管道的幾何尺寸息息相關。數據表明，旋渦的分離頻率同流量存在正相關性，此頻率可通過傳感器獲得。以上管道蒸汽渦街計量表與卡門渦街的關系可從圖1看出，二者有如下邏輯關系：
式中：
f 為旋渦分離頻率，Hz ；
S r 為斯特勞哈爾數；
U 1 為旋渦發生體兩側的平均流速，m/s ；
d 為旋渦發生體迎流面的寬度，m；
U 為被測介質來流的平均流速，m/s ；
m 為旋渦發生體兩側弓形面積與管道橫截面面積之比。不可壓縮流體中，由于流體密度 r 不變，由連續性方程可得到： m = U / U 1 。
式中：K 為管道蒸汽渦街計量表的儀表系數，1 /m 3 。通過式（3）不難看出，儀表系數 K 是管道蒸汽渦街計量表的計量特性的定量表征，數據表明，其儀表系數只和其機械結構與斯特勞哈爾數有關，同來流流量并無相關性。
研究發現，蒸汽對管道蒸汽渦街計量表計量特性存在較大影響。可總結為三個方面：
*一，從公式（3）中能夠得出，機械結構尺寸 D 、m 、 d 以及斯特勞哈爾數 S r 這些參數與K值大小存在較大關聯性。基于物理原理研究發現，在流體介質條件存在差異情況下，機械結構尺寸的改變一般是與溫度的改變引發的熱脹冷縮效應息息相關。
*二，雷諾數對斯特勞哈爾數 S r 產生較大影響，前者又與粘度密切相關，而粘度的差異性又取決于流體的差異，既而引發斯特勞哈爾數 S r 的區別。
*三，公式（3）的推導過程是以不可壓縮流體為前提的，當換作氣體介質時，由于可壓縮性的區別或許會引發儀表系數產生誤差。以上三個因素對于管道蒸汽渦街計量表的影響將在下一節進一步探討。
2 蒸汽介質斯特勞哈爾數的影響
嚴格而言，斯特勞哈爾數是一種相似準則，是在討論流體力學中物理相似和模化是引入的概念。其是用來表征旋渦頻率和阻流體特征尺寸、流速關系的。在特定雷諾數區間中，旋渦的分離頻率和旋渦發生體與管道的幾何尺寸密切相關，換言之斯特勞哈數可視為定量。
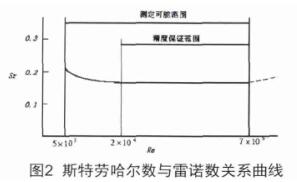
由圖2可看出，在 R eD =2×10 4 7×10 6 區間內，斯特勞哈數是定值，此也是儀表的正常工作區間。
現實情形下， S r 即便在 R eD =2×10 4 7×10 6 區間內，也與 R eD 的改變發生變化，參照1989年日本制訂的管道蒸汽渦街計量表工業標準JISZ8766《管道蒸汽渦街計量表——流量測量方法》。2002年加以修訂，把管道蒸汽渦街計量表發生體的固定形式歸為兩種，《標準》規定的旋渦設計，發生體依據插入測量管頂端固定與否區別為標準1型與標準2型，它們的 S r 值存在較小區別，詳見表1數據。
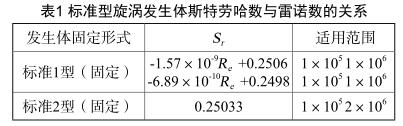
標準2型 S r 的平均值是0.25033，它的標準偏差是0.12%；而標準1型為0.3%，現階段我國一般廣泛采用標準1型。而標準2型在日本橫河儀表研制的管道蒸汽渦街計量表普遍采用。
通過雷諾數的推導公式不難得出，檢測時，蒸汽和空氣因為粘度的區別，會引發雷諾數存在差異。參照一般實驗情況下三類流體介質的工況差異，它們的運動粘度詳見表2：
式中：
表征介質密度；
D 表征管徑；
u 表征流速；
表征介質動力粘度；
v 表征介質運動粘度。
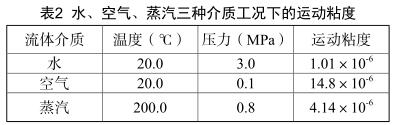
通過以上各參數數據不難發現，水的運動粘度*低，空氣*高，蒸汽介于二者之間。三者比例是1：15：4。所以若使雷諾數一致，應使水的流速*小，空氣*大，蒸汽在區間取值。在對儀表的系數進行檢定過程中，通常應考慮雷諾數一致時，真實測量過程中的差異性誤差。尤其在蒸汽的測量時，儀表量程的選型是參照在空氣介質下測量獲得的體積流量區間與蒸汽的密度乘積，推導出蒸汽的體積流量區間。這種算法會引發差異性介質下雷諾數的區間差異。細致分析上表可得出，只要雷諾數在既定范圍內，檢定過程中并不會由于介質的不同造成較大的誤差，這個影響可不考慮。但雷諾數不可超出規定區間，否則會引發 S r 的較大差異，造成誤差。
通過表3不難發現，要得出管道蒸汽渦街計量表基于*低流量的限雷諾數，口徑一致情況下三類介質的*小流速應滿足1.0：4.0：15.0的大致比例。所以不可以將空氣介質下的體積流量區間等同于蒸汽介質下的數值。
3 蒸汽介質物理特性影響分析
1873年，荷蘭**物理學家范德瓦爾斯特實驗室中，發現了水蒸氣的物理性質，得出氣體分子間有著一定作用力，繼而推導出氣體的狀態方程以輔助理論驗證，這就是**的范德瓦爾斯特氣體狀態方程。進一步研究發現，水蒸汽的分子的體積和相互的作用力比較大，無法以理想的氣體狀態方程加以表征。參照范德瓦爾斯特公式（5）的計算過程：
式中：
p 為壓強；
V 為1摩爾氣體的體積；
R 為普適氣體常數；
a 為度量分子間引力的參數；
b 為1摩爾分子本身包含的體積之和。
以上公式（5）中因子 a 和 b 的值因氣體的性質不同而存在差異，一般地，氣體的分子間引力參數 a 與 b 分子體積 表述如表3所示。
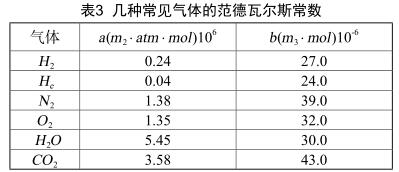
范德瓦爾斯特提出，氣體分子間的吸引力與間距存在負相關性，也就是密度的概念。把此理論使用在管道蒸汽渦街計量表的測量過程中，通過表中的數據不難發現，水蒸汽分子間的吸引力a的數值較大，相當于氧氣與氮氣的4倍多。所以，在測量實際氣體時，基于同等壓力條件，水的分子間的吸引力的數值較蒸汽與空氣大得多，而蒸汽又顯著大于空氣。用管道蒸汽渦街計量表進行測量時，發生體兩側的位置因為流速加大，引起靜壓力減小，體積擴張，流體密度隨之減小，而水介質由于分子間作用力大，并無明顯膨脹情況。蒸汽的分子間的吸引力比空氣大，所以前者膨脹性更低，密度變化也更小。參考流量的連續性方程得出，因為空氣密度變化更大，所以它的發生體兩側的流量變化較蒸汽介質更大，所以它的儀表系數比蒸汽介質變化更顯著。而氣體的可壓縮性與等嫡指數是其內在機理，這和我們的理論研究結果相互印證。
到了二十世紀80年代，因為工業生產的推動，管道蒸汽渦街計量表得以廣泛采用，但缺點是對于蒸汽介質上的測試仍是空白，只可進行管道蒸汽渦街計量表的構造方式、DSP、流量量程、管道材質等方面加以升級，增強了管道蒸汽渦街計量表的在液體與空氣中的測量準度。由于在蒸汽介質方面的探索上存在盲區，在流量精度測量上長期以來備受業內人士的質疑。管道蒸汽渦街計量表雖然技術上有了改進，但有待進一步改良，不管是在理論還是應用層面上均有諸多工作要做。近些年，**范圍內的業內人士對于管道蒸汽渦街計量表實施了多次探索，研究成果值得肯定。
蒸汽流量量值體系的溯源是保證蒸汽流量測量準確的關鍵。本文基于流體力學、熱力學以及管道蒸汽渦街計量表旋渦的產生機理，分析不同介質對管道蒸汽渦街計量表的計量特性的影響，介質粘度的不同導致了三種介質測試下雷諾數的不同，影響到斯特勞哈數差異。但對管道蒸汽渦街計量表的儀表系數影響不大，可忽略其影響。介質粘度的不同會導致流量范圍的不同。該分析將有利于提高管道蒸汽渦街計量表測量蒸汽流量的計量準確度。
1 蒸汽介質的影響因素
所謂管道蒸汽渦街計量表(亦稱旋渦流量計)，其工作機理是“卡門渦街”，是一類流體振蕩式的測量儀器。“卡門渦街”的原理是：待測管道流體中放進一根(或數根)非流線型截面的旋渦發生體，等到雷諾數到達特定數值，在旋渦發生體兩側分離出兩串交錯有序的旋渦，此過程具有交替性，我們將這種旋渦叫作卡門渦街。在特定雷諾數范圍之間，旋渦的分離頻率同旋渦發生體與管道的幾何尺寸息息相關。數據表明，旋渦的分離頻率同流量存在正相關性，此頻率可通過傳感器獲得。以上管道蒸汽渦街計量表與卡門渦街的關系可從圖1看出，二者有如下邏輯關系：
式中：
f 為旋渦分離頻率，Hz ；
S r 為斯特勞哈爾數；
U 1 為旋渦發生體兩側的平均流速，m/s ；
d 為旋渦發生體迎流面的寬度，m；
U 為被測介質來流的平均流速，m/s ；
m 為旋渦發生體兩側弓形面積與管道橫截面面積之比。不可壓縮流體中，由于流體密度 r 不變，由連續性方程可得到： m = U / U 1 。
式中：K 為管道蒸汽渦街計量表的儀表系數，1 /m 3 。通過式（3）不難看出，儀表系數 K 是管道蒸汽渦街計量表的計量特性的定量表征，數據表明，其儀表系數只和其機械結構與斯特勞哈爾數有關，同來流流量并無相關性。
研究發現，蒸汽對管道蒸汽渦街計量表計量特性存在較大影響。可總結為三個方面：
*一，從公式（3）中能夠得出，機械結構尺寸 D 、m 、 d 以及斯特勞哈爾數 S r 這些參數與K值大小存在較大關聯性。基于物理原理研究發現，在流體介質條件存在差異情況下，機械結構尺寸的改變一般是與溫度的改變引發的熱脹冷縮效應息息相關。
*二，雷諾數對斯特勞哈爾數 S r 產生較大影響，前者又與粘度密切相關，而粘度的差異性又取決于流體的差異，既而引發斯特勞哈爾數 S r 的區別。
*三，公式（3）的推導過程是以不可壓縮流體為前提的，當換作氣體介質時，由于可壓縮性的區別或許會引發儀表系數產生誤差。以上三個因素對于管道蒸汽渦街計量表的影響將在下一節進一步探討。
2 蒸汽介質斯特勞哈爾數的影響
嚴格而言，斯特勞哈爾數是一種相似準則，是在討論流體力學中物理相似和模化是引入的概念。其是用來表征旋渦頻率和阻流體特征尺寸、流速關系的。在特定雷諾數區間中，旋渦的分離頻率和旋渦發生體與管道的幾何尺寸密切相關，換言之斯特勞哈數可視為定量。
由圖2可看出，在 R eD =2×10 4 7×10 6 區間內，斯特勞哈數是定值，此也是儀表的正常工作區間。
現實情形下， S r 即便在 R eD =2×10 4 7×10 6 區間內，也與 R eD 的改變發生變化，參照1989年日本制訂的管道蒸汽渦街計量表工業標準JISZ8766《管道蒸汽渦街計量表——流量測量方法》。2002年加以修訂，把管道蒸汽渦街計量表發生體的固定形式歸為兩種，《標準》規定的旋渦設計，發生體依據插入測量管頂端固定與否區別為標準1型與標準2型，它們的 S r 值存在較小區別，詳見表1數據。
標準2型 S r 的平均值是0.25033，它的標準偏差是0.12%；而標準1型為0.3%，現階段我國一般廣泛采用標準1型。而標準2型在日本橫河儀表研制的管道蒸汽渦街計量表普遍采用。
通過雷諾數的推導公式不難得出，檢測時，蒸汽和空氣因為粘度的區別，會引發雷諾數存在差異。參照一般實驗情況下三類流體介質的工況差異，它們的運動粘度詳見表2：
式中：
表征介質密度；
D 表征管徑；
u 表征流速；
表征介質動力粘度；
v 表征介質運動粘度。
通過以上各參數數據不難發現，水的運動粘度*低，空氣*高，蒸汽介于二者之間。三者比例是1：15：4。所以若使雷諾數一致，應使水的流速*小，空氣*大，蒸汽在區間取值。在對儀表的系數進行檢定過程中，通常應考慮雷諾數一致時，真實測量過程中的差異性誤差。尤其在蒸汽的測量時，儀表量程的選型是參照在空氣介質下測量獲得的體積流量區間與蒸汽的密度乘積，推導出蒸汽的體積流量區間。這種算法會引發差異性介質下雷諾數的區間差異。細致分析上表可得出，只要雷諾數在既定范圍內，檢定過程中并不會由于介質的不同造成較大的誤差，這個影響可不考慮。但雷諾數不可超出規定區間，否則會引發 S r 的較大差異，造成誤差。
通過表3不難發現，要得出管道蒸汽渦街計量表基于*低流量的限雷諾數，口徑一致情況下三類介質的*小流速應滿足1.0：4.0：15.0的大致比例。所以不可以將空氣介質下的體積流量區間等同于蒸汽介質下的數值。
3 蒸汽介質物理特性影響分析
1873年，荷蘭**物理學家范德瓦爾斯特實驗室中，發現了水蒸氣的物理性質，得出氣體分子間有著一定作用力，繼而推導出氣體的狀態方程以輔助理論驗證，這就是**的范德瓦爾斯特氣體狀態方程。進一步研究發現，水蒸汽的分子的體積和相互的作用力比較大，無法以理想的氣體狀態方程加以表征。參照范德瓦爾斯特公式（5）的計算過程：
式中：
p 為壓強；
V 為1摩爾氣體的體積；
R 為普適氣體常數；
a 為度量分子間引力的參數；
b 為1摩爾分子本身包含的體積之和。
以上公式（5）中因子 a 和 b 的值因氣體的性質不同而存在差異，一般地，氣體的分子間引力參數 a 與 b 分子體積 表述如表3所示。
范德瓦爾斯特提出，氣體分子間的吸引力與間距存在負相關性，也就是密度的概念。把此理論使用在管道蒸汽渦街計量表的測量過程中，通過表中的數據不難發現，水蒸汽分子間的吸引力a的數值較大，相當于氧氣與氮氣的4倍多。所以，在測量實際氣體時，基于同等壓力條件，水的分子間的吸引力的數值較蒸汽與空氣大得多，而蒸汽又顯著大于空氣。用管道蒸汽渦街計量表進行測量時，發生體兩側的位置因為流速加大，引起靜壓力減小，體積擴張，流體密度隨之減小，而水介質由于分子間作用力大，并無明顯膨脹情況。蒸汽的分子間的吸引力比空氣大，所以前者膨脹性更低，密度變化也更小。參考流量的連續性方程得出，因為空氣密度變化更大，所以它的發生體兩側的流量變化較蒸汽介質更大，所以它的儀表系數比蒸汽介質變化更顯著。而氣體的可壓縮性與等嫡指數是其內在機理，這和我們的理論研究結果相互印證。